Question

Does anyone know this?!?

Answer 1

`\boxed{y = -(4)/(9)x + 2}`

`\boxed{y = -(4)/(9)x}`

`\boxed{y = -(4)/(9)x -6}`

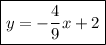
Explanation:

The equation of a line in slope-intercept form is
y = mx + c

where m = slope and c is the y-intercept i.e. the value of y when x = 0

Slope m = (y₂ - y₁)/(x₂ - x₁) where (x₁, y₁) and (x₂, y₂) are any two points on the line

In this case we can see that the given line passes through two distinct points (-9, 0) and (0, -4) as shown in Line 1 of the attached Figure 1

Therefore slope of this line is

`(-4 - 0)/(0 - (-9)) = -(4)/(9)`

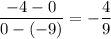
Since -4 is the y-intercept (when x = 0) then the equation of the line in slope intercept form is

`y = - (4)/(9)x - 4` (Line 1)

The next thing to note is that all lines parallel to Line 1 will have the exact same slope but the y intercepts will be different

For a y-intercept of (0, 2) the line equation will be

`\boxed{y = -(4)/(9)x + 2}`

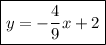
For y-intercept of (0, 0) the line equation will be

`y = -(4)/(9)x + 0 \; \text{or\;simply } \boxed{y = -(4)/(9)x}`

For y-intercept of (0, -6) the line equation will be

`\boxed{y = -(4)/(9)x -6}`

All three lines and the original line are plotted in the second figure