Question

What is the inverse of the function

Answer 1

`\boxed{\sf g^(-1)(x) = (5)/(4)(x - 3) }`

Explanation:

`\sf g(x) = (4)/(5)x + 3`

The inverse of the function is the function that reverses the input and output of g(x).

In other words, if y = g(x), then the inverse function, denoted by
`g^(-1)(x)` , gives us
`\sf x = g^(-1)(y)`

To find the inverse of g(x), we can swap the variables x and y and solve the resulting equation for y.

`y = (4)/(5)x + 3`

Swap the value;

`\sf x = (4)/(5)y + 3`

`\sf x - 3 = (4)/(5)y`

`\sf (5)/(4)(x - 3) = y`

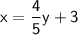
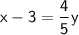
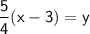
Therefore, the inverse of the function is the function:

`\boxed{\sf g^(-1)(x) = (5)/(4)(x - 3) }`