Question

Please solve the rational inequality: (x-5)^2/x^2-16 greater than or equal to 0. But my teacher told me the answer was (-infinity, -4) union (4, positive infinity).

Answer 1

(-∞, -4) ∪ (4, ∞)

Explanation:

Given rational inequality:

`((x-5)^2)/(x^2-16)\geq 0`

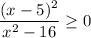
To solve the given rational inequality, begin by factoring the denominator x² - 16 using the difference of two squares:

`((x-5)^2)/((x+4)(x-4))\geq 0`

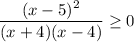
Find the roots by setting the numerator equal to zero and solving for x:

`(x-5)^2=0 \implies \boxed{x=5}`

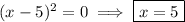
Find the restrictions by setting the denominator equal to zero and solving for x:

`(x+4)(x-4)=0 \implies \boxed{x=-4,\;x=4}`

Therefore, the critical values are x = 5, x = -4 and x = 4.

So, we need to test a value for each of the following intervals:

• (-∞, -4)
• (-4, 4)
• (4, 5)
• (5, ∞)

Create a sign chart (see attachment), using a closed dot for the root (x = 5) and open dots for the restrictions (x = -4 and x = 4).

Choose a test value for each region, including one to the left of all the critical values and one to the right of all the critical values.

• Test values: -5, 0, 4.5, 6

For each test value, determine if the function is positive or negative:

`f(-5)=(((-5)-5)^2)/((-5)^2-16)=(100)/(9)\leftarrow \sf positive`

`f(0)=(((0)-5)^2)/((0)^2-16)=(25)/(-16)=-(25)/(16)\leftarrow \sf negative`

`f(4.5)=(((4.5)-5)^2)/((4.5)^2-16)=((1)/(4))/((17)/(4))=(1)/(17)\leftarrow \sf positive`

`f(6)=(((6)-5)^2)/((6)^2-16)=(1)/(20)\leftarrow \sf positive`

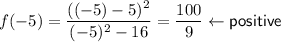
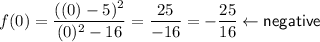
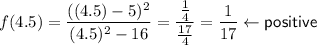
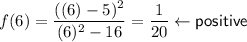
Record the results on the sign chart for each region (see the attachment).

As we need to find the values for which f(x) ≥ 0, shade the appropriate regions (zero or positive) on the sign chart.

Therefore, the solution set is (-∞, -4) ∪ (4, ∞).