Question

A gas has a temperature of 34.9 degrees C and a volume of 70.0 L. If the temperature increases to 86.8 degreesC , what is its final volume ?

Answer 1

81.8 L

Step-by-step explanation:

Ideal gas law:

PV = nR T

V = nR/P * T since nr and P are constant , this becomes

V = k T where k is a proportionality constant ====> then: V/T = k

so:

V1/T1 = V2/T2 ( NOTE : T must be in K)

V2 = T2 ( V1/T1) = ( 86.8 + 273.15) ( 70.0) /(34.9 + 273.15) = 81.8 L

Answer 2

Its final volume is 81.8 L

Explanation

Given;

Initial temperature, T₁ = 34.9°C = (34.9 + 273.15 K) = 308.05 K

Initial volume, V₁ = 70.0 L

Final temperature, T₂ = 86.8°C = ( 86.8 + 273.15 K) = 359.95 K

What to find:

The final volume at 86.8°C.

Step-by-step solution:

The final volume, V₂ can be calculated using Charle's law formula below:

`\begin{gathered} (V_1)/(T_1)=(V_2)/(T_2) \\ \\ \Rightarrow V_2=(V_1T_2)/(T_1) \end{gathered}`

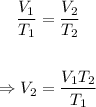
Putting the values of the given parameters into the formula, we have

`V_2=(70.0L*359.95K)/(308.05K)=81.8\text{ }L`

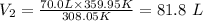
Hence, if the temperature of the gas increases to 86.8 degrees C, its final volume is 81.8 L