Answer
Its final volume is 81.8 L
Explanation
Given;
Initial temperature, T₁ = 34.9°C = (34.9 + 273.15 K) = 308.05 K
Initial volume, V₁ = 70.0 L
Final temperature, T₂ = 86.8°C = ( 86.8 + 273.15 K) = 359.95 K
What to find:
The final volume at 86.8°C.
Step-by-step solution:
The final volume, V₂ can be calculated using Charle's law formula below:

Putting the values of the given parameters into the formula, we have
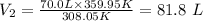
Hence, if the temperature of the gas increases to 86.8 degrees C, its final volume is 81.8 L