Question

What is the slope of the line that passes through the points (−6,−6) and(−9,−5)? Write your answer in simplest form.

Answer 1

To find the slope (\(m\)) of the line passing through the points \((-6, -6)\) and \((-9, -5)\), we'll use the formula:

\[m = \frac{{y_2 - y_1}}{{x_2 - x_1}}\]

Substitute the coordinates:

\[m = \frac{{-5 - (-6)}}{{-9 - (-6)}}\]

Simplify:

\[m = \frac{{1}}{{-3}}\]

So, the slope of the line is \(-\frac{1}{3}\) in simplest form.

Explanation:

Answer 2

`\sf - (1)/(3)`

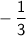
Explanation:

To find the slope of the line that passes through the points (-6, -6) and (-9, -5), we can use the slope formula:

`\boxed{\boxed{\sf m = (y_2 - y_1)/(x_2 - x_1)}}`

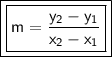
Where:

m is the slope of the line,

`(x_1, y_1)` are the coordinates of the first point (-6, -6), and

`\sf (x_2, y_2)` are the coordinates of the second point (-9, -5).

Substitute the values into the formula:

`\sf m = (-5 - (-6))/(-9 - (-6))`

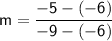
Now, simplify:

`\sf m = (-5 + 6)/(-9 + 6)`

`\sf m =- (1)/(3)`

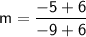
So, the slope of the line that passes through the points (-6, -6) and (-9, -5) is
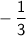`\sf - (1)/(3)` in simplest form.