Question

How to rewrite x^2+16x+ 71 in vertex form

Answer 1

To rewrite the quadratic equation \(x^2 + 16x + 71\) in vertex form (\(a(x-h)^2 + k\)), we'll complete the square. Here are the steps:

1. Start with the original equation:

\(x^2 + 16x + 71\)

2. Complete the square for the quadratic term and the linear term:

\(x^2 + 16x + \underline{64} + 71 - \underline{64}\)

We added and subtracted 64 to keep the equation balanced. Remember, adding 64 inside the parentheses is equivalent to adding \(a \cdot 64\) to the equation, where \(a\) is the coefficient of the quadratic term.

3. Rewrite the expression:

\((x + 8)^2 + 7\)

The equation \(x^2 + 16x + 71\) in vertex form is \((x + 8)^2 + 7\). This form makes it easier to identify the vertex, which is \((-8, 7)\).

Explanation:

Answer 2

`\sf (x + 8)^2 + 7`

Explanation:

To rewrite the quadratic equation
`\sf y = x^2 + 16x + 71` in vertex form, which has the form
`\boxed{\sf a(x - h)^2 + k}` , we need to complete the square. Here are the steps to do that:

Begin with the given quadratic equation:

`\sf x^2 + 16x + 71`

To complete the square, focus on the quadratic terms x² and 16x.

Take half of the coefficient of the linear term (16/2 = 8), square it (8² = 64), and add it both inside and outside the parentheses.

Rewrite the equation by adding and subtracting the value we found in step 3:

`\sf x^2 + 16x + 64 - 64 + 71`

Now, the expression inside the parentheses is a perfect square trinomial:

`\sf x^2 + 16x + 64 = (x + 8)^2`

Simplify the equation:

`\sf (x + 8)^2 + 71 - 64`

`\sf (x + 8)^2 + 7`

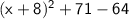
So, the vertex form of the quadratic equation is:

`\sf (x + 8)^2 + 7`