Question

The sides of a rectangle are in a ratio of 5:7 and the perimeter is 72. Find the area of the rectangle.

Answer 1

Since the sides of the rectangle are in ratio 5: 7

Insert x in the 2 terms of the ratio and find its perimeter using them

`\begin{gathered} L\colon W=5x\colon7x \\ P=2(L+W) \\ P=2(5x+7x) \\ P=2(12x) \\ P=24x \end{gathered}`

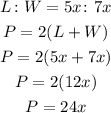
Equate 24x by the given perimeter 72 to find the value of x

`24x=72`

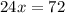
Divide both sides by 24

`\begin{gathered} (24x)/(24)=(72)/(24) \\ x=3 \end{gathered}`

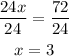
Then the sides of the rectangle are

`\begin{gathered} L=5(3)=15 \\ W=7(3)=21 \end{gathered}`

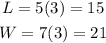
Since the rule of the area of the rectangle is A = L x W, then

`\begin{gathered} A=15*21 \\ A=315 \end{gathered}`

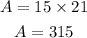
The area of the rectangle is 315 square units