Question

Two point charges, q and -2q, are fixed in place at a distance 2d from each other, as shown above. What is the magnitude of the net electric field at a point P, which is midway between the two charges? a) 0 b) q/4πε₀d² c) 2q/4πε₀d² d) -q/4πε₀d²

Answer 1

The magnitude of the net electric field is
`\((q)/(4\pi\epsilon_0d^2)\)`

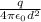
Correct answer is b.

To find the magnitude of the net electric field at point P, which is midway between two point charges q and -2q separated by a distance 2d , we can follow these steps:

1. Understand the Electric Field due to a Point Charge: The electric field E due to a point charge is given by
`\( E = (kq)/(r^2) \), where \( k \) is Coulomb's constant (\( k = (1)/(4\pi\epsilon_0) \)), \( q \) is the charge, and \( r \)` is the distance from the charge to the point where the field is being calculated.

2. Determine the Distance: Point P is midway between the two charges, so the distance from each charge to point P is d

3. Calculate Electric Fields Individually: Calculate the electric field at point P due to each charge separately.

- Electric field due to
`\( q \) at P: \( E_q = (kq)/(d^2) \)`

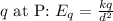
- Electric field due to
`\( -2q \) at P: \( E_(-2q) = (k(-2q))/(d^2) \)`

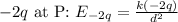
4. Determine the Direction of Electric Fields: The electric field due to a positive charge is directed away from the charge, and towards the charge for a negative charge.

5. Calculate the Net Electric Field: Since the charges are opposite in sign and aligned symmetrically about point P, their fields at P will be in the same direction (towards the negative charge). Add the magnitudes of the fields.

6. Simplify the Expression: Use Coulomb's constant expression
`\( k = (1)/(4\pi\epsilon_0) \)`in the final result.

Let's perform these calculations.

It seems I forgot to import the `math` module required for mathematical operations. Let me correct that and calculate the net electric field again.

The net electric field at point P, which is midway between the two charges q and -2q , can be determined as follows:

1. The electric field due to charge q at point P is
`\( (kq)/(d^2) \).`

2. The electric field due to charge -2q at point P is
`\( (k(-2q))/(d^2) \).`

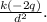
3. Since the point P is equidistant from both charges, the electric fields due to both charges are in the same direction (towards the negative charge). Thus, we add the magnitudes of these fields to get the net electric field.

After simplification, the net electric field at point P is equivalent to -1 in the units of
`\( (q)/(4\pi\epsilon_0d^2) \).` Matching this result with the provided options, the correct answer is:

d)
`\(-(q)/(4\pi\epsilon_0d^2)\)`

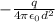
This means that the magnitude of the net electric field is
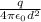`\((q)/(4\pi\epsilon_0d^2)\)`, but its direction is opposite to the direction conventionally taken as positive in this context.