Question

Name Danielle Klein Datealillar S4: Linear Equations, Functions, and Inequalities T6: Finding Solution Sets to Systems of Equations Using Substitution and Graphing Independent Practice 1. Last Monday, two law students met up at Café Literatura after school to read the pages they were assigned in the Legal Methods class. Alejandro can read 1 page per minute, and he has read 28 pages so far. Carly, who has a reading speed of 2 pages per minute, has read 12 pages so far. Part A: Define the variables and write two equations to represent the number of pages that each student read. DE 4 Variables: X-Minutes they real they head Alejandro:X-XF28 x= Number of payes Carly:apGraph both equations , find when Alejandro has read more pages than Carly, and when they have read the same amount of pages.

Answer 1

Let t be the time and P be the number of pages that each students has read. In both cases, the equation that relates P and t is a linear equation. The slope-intercept form of the equation of a line is:

`y=mx+b`

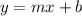
Where m represents the rate of change of y with respect to x and b represents the initial value when x=0.

In this case, where P represents the number of pages and t represents the time, the relation can be written as:

`P=mt+b`

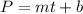
Adjust the paramenters m and b for each student.

Since Alejandro can read 1 page per minute, then the rate of change of the number of pages with respect to time is 1. Since he has read 28 pages so far, then the initial value is 28. The number of pages that Alejandro reads, is:

`P=t+28`

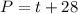
Since Carly can read 2 pages per minute, the rate of change is 2. Since she has read 12 pages so far, the initial value is 12. The equation for Carly, is:

`P=2t+12`

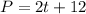
To graph each equation, evaluate it on two different values of t to find the corresponding values of P.

For Alejandro, let's use t=0 and t=1:

`\begin{gathered} t=0\Rightarrow P=0+28\Rightarrow P=28 \\ t=1\Rightarrow P=1+28\Rightarrow P=29 \end{gathered}`

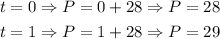
Plot the points (0,28) and (1,29) in a coordinate plane:

Then, draw a line through them:

Do the same for Carly's equation. We can see that two points on the line would be (0,12) and (1,14):

To find when has Alejandro read more pages than Carly, write an inequality. After t minutes, Alejandro has read t+28 pages, and Carly has read 2t+12 pages. We want t+28 to be greater than 2t+12, then:

`t+28>2t+12`

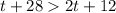
Substract t from both sides:

`\begin{gathered} t+28-t>2t+12-t \\ \Rightarrow28>t+12 \end{gathered}`

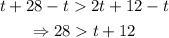
Substract 12 from both sides:

`\begin{gathered} 28-12>t+12-12 \\ \Rightarrow16>t \end{gathered}`

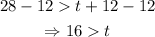
Therefore, whenever t is less than 16 minutes, Alejandro has read more pages than Carly.

Notice that if we replace the ">" sign for a "=" sign, we would find that they have read the same amount of pages when t=16 minutes.