Answer:
Hi,
Explanation:
1.
If x 2 + 2x -3 is a factor of the polynomial f(x) = 2x 3 + ax 2 + ax – b, where a and b are constants, find the values of a and b.

Let's divide f(x) by x-1 and then by x+3
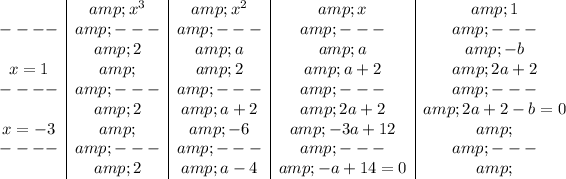

(i) Factorize f(x) completely

(ii) State the zeros of f(x)
Zeros are 1,-3,-5
(iii) Find the remainder when f(x) is divided by (x-5)
remainder is 0
2.
Find the equation whose roots are 1, 2 and 3.
E(x)=(x-1)(x-2)(x-3)=
3. Given the equation 4(y² - 2)² = k(y – 1) , where k is constant.