We are given the following system of equations:
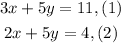
We can solve this system of equations using the method of elimination. To do that we will multiply equation (2) by -1:
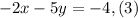
Now we add equations (1) and (3):
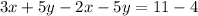
Adding like terms:
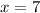
Now we replace the value of "x" is equation (1):
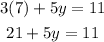
Now we subtract 21 to both sides:
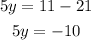
Dividing both sides by 5:
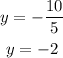
Therefore, the solution of the system is:
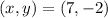
For the second system of equations:
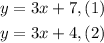
These equations represent two lines with the same slope, and therefore, parallel lines. Since they are parallel lines this means that the system has no solutions.