Question

Two systems of equations are given below.For each system, choose the best description of its solution.If applicable, give the solution.System AThe system has no solution.The system has a unique solution:3x + 5y = 112x + 5y=4(x, y) = (1,5The system has infinitely many solutions.System BThe system has no solution.The system has a unique solution:y = 3x + 7y = 3x + 4(x, y) = (2, 2)The system has infinitely many solutions.

Answer 1

We are given the following system of equations:

`\begin{gathered} 3x+5y=11,(1) \\ 2x+5y=4,(2) \end{gathered}`

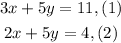
We can solve this system of equations using the method of elimination. To do that we will multiply equation (2) by -1:

`-2x-5y=-4,(3)`

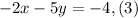
Now we add equations (1) and (3):

`3x+5y-2x-5y=11-4`

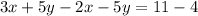
Adding like terms:

`x=7`

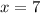
Now we replace the value of "x" is equation (1):

`\begin{gathered} 3(7)+5y=11 \\ 21+5y=11 \end{gathered}`

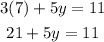
Now we subtract 21 to both sides:

`\begin{gathered} 5y=11-21 \\ 5y=-10 \end{gathered}`

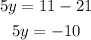
Dividing both sides by 5:

`\begin{gathered} y=-(10)/(5) \\ y=-2 \end{gathered}`

Therefore, the solution of the system is:

`(x,y)=(7,-2)`

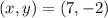
For the second system of equations:

`\begin{gathered} y=3x+7,(1) \\ y=3x+4,(2) \end{gathered}`

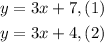
These equations represent two lines with the same slope, and therefore, parallel lines. Since they are parallel lines this means that the system has no solutions.