Decomposing the tension into vertical and horizontal components, and considering vertical force equilibrium, the tension in the supporting wire is approximately 679.94 N, maintaining stability in the system with a hanging sign weighing 215 N on a 175 N beam.
1. Decompose Tension into Components:
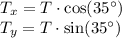
2. Vertical Force Equilibrium:
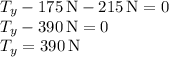
3. Tension in the Wire:
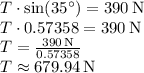
Therefore, the tension in the supporting wire is approximately
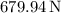 .
.