As given by the question
There are given that the total number of boys is 8 and total numbers of girls is 6.
Now,
Since there are two competitions, one for boys and one for girls and we want all the possible results we will calculate the possible combination for the boys and multiply them by the possible combination for the girls.
Then,
For the boys:
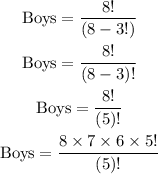
Then,
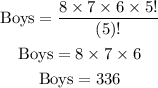
Now,
For the girl:
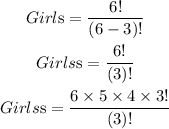
Then,
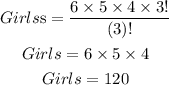
Now,
A total number of possible results:
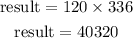
Hence, the ways are 40320.