Question

Consider the two linear expressions.

−(−1/2−6x−3) and 3.5−6x

Are the two linear expressions equivalent?

Drag a word or phrase to the box to correctly complete the statement.

PLEASE HURRY THIS IS A K12 TEST

Answer 1

Not equivalent

Explanation:

Two linear expressions are equivalent if they have the same slope and the same y-intercept.

The first linear expression can be simplified as follows:

Open the parenthesis by distributing minus and simplify like terms

`\sf - \left(-(1)/(2)-6x-3\right) = (1)/(2)+6x+3 \\\\ = 6x+(1+3\cdot 2 )/(2) \\\\ =6x + (7)/(2) \textsf{ Or} 6x + 3.5`

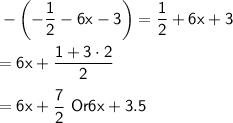
The second linear expression is already in its simplest form:

`\sf 3.5-6x = -6x+3.5`

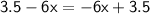
Let's analyse it.

The slope of the first expressions is 6 and second one is -6, and the y-intercept of the first expression is 3.5.

Since the slope are not same.

So, the two linear expressions are not equivalent.