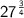Question

QUESTION in pic below

Answer 1

c

Explanation:

Answer 2

`\sf 27^(3)/(4)`

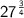
Explanation:

To rewrite the expression
`27^(1)/(2)\cdot 27^(1)/(4)` in terms of 27, we can use the following property of exponents:

`\boxed{\boxed{\sf a^m \cdot a^n = a^(m+n) }}`

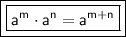
This property states that when multiplying two powers with the same base, we can add the exponents together.

Therefore, we can rewrite the expression as follows:

`\sf 27^(1)/(2)\cdot 27^(1)/(4)= 27^{(1)/(2)+(1)/(4)}`

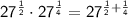
Adding the exponents, we get:

`\sf 27^{(1)/(2)+(1)/(4)} = 27^{ (2+1)/(4)} = 27^(3)/(4)`

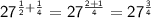
Therefore, the expression is:

`\sf 27^(3)/(4)`