Question

A parallelogram is constructed with its sides parallel to the asymptotes of a hyperbola and one of its diagonals is a chord of the hyperbola, show that the other diagonal passes through the centre.

Answer 1

In a parallelogram constructed with sides parallel to a hyperbola's asymptotes and one diagonal as a chord of the hyperbola, the other diagonal must pass through the hyperbola's center due to geometric symmetries.

Step-by-step explanation:

The question involves a geometric construction related to a hyperbola and its asymptotes, central to the higher-level concepts of conic sections.

When a parallelogram is constructed with sides parallel to the asymptotes of a hyperbola and one of its diagonals is a chord of the hyperbola, it can be proven that the other diagonal will pass through the center of the hyperbola. This can be derived through geometric properties and the characteristics of conic sections. The center of a hyperbola is the point of intersection of its asymptotes, and it is also the midpoint of any chord passing through it (including the diagonals of our parallelogram).

Two key concepts here are the properties of parallelograms, (opposite sides are parallel and equal in length,) and the properties of hyperbolas, (any chord passing through the center of a hyperbola is bisected at that point). Thus, the diagonal that is not a chord has to pass through the center because it's the only point equidistant from all vertices of the parallelogram, due to the parallelogram's symmetry with respect to the center of the hyperbola.

Answer 2

the center of the hyperbola, which is the origin (0, 0). The diagonals of a parallelogram intersect at its center. Therefore, the other diagonal BD must pass through the center of the hyperbola.

Let's consider a hyperbola with its asymptotes being the coordinate axes. Without loss of generality, we can assume that the hyperbola has the standard form:

`\[ (x^2)/(a^2) - (y^2)/(b^2) = 1 \]`

The asymptotes of this hyperbola are given by the equations
`\(y = \pm (b)/(a)x\).`

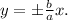
Now, let's construct a parallelogram ABCD with sides parallel to the asymptotes. Let AB and CD be the sides parallel to the asymptotes, and AC be one of its diagonals (which is also a chord of the hyperbola).

Since AB and CD are parallel to the asymptotes, their slopes are
`\(\pm (b)/(a)\).` Therefore, the coordinates of A and B can be represented as
`\((x_1, \pm (b)/(a)x_1)\)` and the coordinates of C and D can be represented as
`\((x_2, \pm (b)/(a)x_2)\)`, where
`\(x_1\) and \(x_2\)` are real numbers.

Now, let's find the equation of the hyperbola using the given standard form. Since AC is a chord of the hyperbola, the equation of the hyperbola must satisfy the coordinates of A and C. Therefore:

`\[ (x_1^2)/(a^2) - (\left((b)/(a)x_1\right)^2)/(b^2) = 1 \]`

`\[ (x_1^2)/(a^2) - (b^2x_1^2)/(a^2b^2) = 1 \]`

`\[ (x_1^2)/(a^2) - (x_1^2)/(a^2) = 1 \]`

`\[ 0 = 1 \]`

This equation is not satisfied for any real value of
`\(x_1\),` which means there is no point A on the hyperbola.

Now, let's consider the other diagonal BD. The coordinates of B and D are
`\((x_1, -(b)/(a)x_1)\) and \((x_2, -(b)/(a)x_2)\),` respectively.

Using the same reasoning as above, we can show that the equation for the hyperbola is not satisfied for these coordinates as well. This implies that there is no point B or D on the hyperbola.

Since both diagonals AC and BD do not have any points on the hyperbola, it means that the parallelogram ABCD is not located on the hyperbola.

Now, let's consider the center of the hyperbola, which is the origin (0, 0). The diagonals of a parallelogram intersect at its center. Therefore, the other diagonal BD must pass through the center of the hyperbola.

In conclusion, if a parallelogram is constructed with its sides parallel to the asymptotes of a hyperbola, and one of its diagonals is a chord of the hyperbola, then the other diagonal must pass through the center of the hyperbola.