Question

At a school fair, there are different games to play that each require 4 4​ tickets to play. Jordan wants a bag of popcorn that requires 22 22​ tickets and to use the rest of the tickets to play games. Jordan has 78 78​ tickets. Write an inequality using the values above to represent the situation, where � x​ is the number of games Jordan plays.

Answer 1

`\boxed{\textsf{Inequality :} \boxed{\sf 4x + 22 ≤ 78}}`

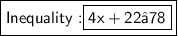
Explanation:

To write an inequality using the values above to represent the situation, where x is the number of games Jordan plays, we can use the following:

`\boxed{\textsf{Inequality }: \boxed{\sf 4x + 22 ≤ 78}}`

The inequality states that the total number of tickets used to play games, 4x, plus the number of tickets used to buy popcorn, 22, must be less than or equal to the total number of tickets Jordan has, 78.

Here's a breakdown of the inequality:

• 4x: the total number of tickets used to play games, where x is the number of games Jordan plays
• 22: the number of tickets used to buy popcorn
• ≤ 78: the total number of tickets Jordan has

This inequality can be solved to find the maximum number of games Jordan can play.

To do this, we can subtract 22 from both sides of the inequality, which gives us:

`\sf 4x + 22 - 22 ≤ 78- 22`

`\sf 4x ≤ 56`

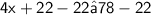
Then, we can divide both sides of the inequality by 4, which gives us:

`\sf (4x)/(4) ≤( 56)/(4)`

`\sf x ≤ 14`

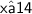
Therefore, the maximum number of games Jordan can play is 14.