Question

the electric current in a circular coil of 2 turns produces a magnetic induction b₁ at its centre. the coil is unwound and is rewound into a circular coil of 5 turns and the same current produces a magnetic induction b₂ at its ratio of b₂/b₁ is: A) B₂ = B₁ B) B₂ = 2B₁ C) B₂ = 5B₁ D) B₂ = 1/5 B₁

Answer 1

The ratio of the magnetic induction B2 to B1 when the number of turns in a coil is increased from 2 to 5 is 2.5, but this correct ratio is not reflected in the answer options provided, indicating a possible error in the options.

Step-by-step explanation:

The magnetic induction at the center of a circular coil is directly proportional to the number of turns in the coil when the electric current and the other factors are held constant. If a coil with 2 turns creates a magnetic induction, B1, at its center, then when the same coil is rewound into 5 turns, the magnetic induction B2 would be (5/2) times larger than B1, assuming all other conditions remain unchanged. Therefore, the ratio B2/B1 would equal the factor by which the number of turns has increased, which is (5/2) or 2.5. Since none of the answer options matches this calculation, there appears to be an error in the list of options provided.

Answer 2

The correct answer is option C)
`\(B_2 = 5B_1\)`.

To find the ratio of magnetic induction
`\(B_2\) to \(B_1\)` when the number of turns in a circular coil changes from 2 to 5 while the current remains the same, we can use the formula for the magnetic field inside a circular coil:

`\(B = \mu_0 \cdot (NI)/(2R)\)`

Where:

`\(B\)` = Magnetic induction

`\(\mu_0\)` = Permeability of free space (a constant)

`\(N\)` = Number of turns in the coil

`\(I\)` = Current

`\(R\)` = Radius of the circular coil

Let's denote the initial coil as Coil 1 and the final coil as Coil 2.

For Coil 1:

`\(N_1 = 2\)` turns

For Coil 2:

`\(N_2 = 5\)` turns (as it's rewound into a circular coil with 5 turns)

The current
`\(I\)` is the same in both cases.

Now, let's find the ratio of
`\(B_2\) to \(B_1\):`

`\((B_2)/(B_1) = (\mu_0 \cdot (N_2I)/(2R))/(\mu_0 \cdot (N_1I)/(2R))\)`

`\(B_2/B_1 = (N_2)/(N_1)\)`

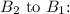
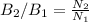
Substitute the values:

`\(B_2/B_1 = (5)/(2) = 2.5\)`

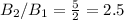
So, the correct answer is:

C)
`\(B_2 = 5B_1\)`