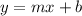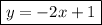Answer:
Explanation:
The slope-intercept form of a linear function is:
→
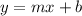
where
is the line's slope and
is it's y-intercept (the
-value of the line when
).
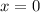Remember that x is the horizontal distance from the origin (0, 0) and y is the vertical distance from the origin.
From the table, we can identify the y-intercept (
) as:
because when the line's
-coordinate is 0, the
-coordinate is 1.
Next, we can find the line's slope using the formula:
slope = rise / run
= Δy / Δx
where Δ means "change in" (i.e. Δx = "change in x").
We can plug in some values from the table to solve for slope. I will use the rows with (-2, 5) and (-1, 3):
slope = (3 - 5) / (-1 - (-2))
= -2 / (-1 + 2)
= -2 / 1
= -2
Finally, we can plug these values into the slope-intercept form equation:
