Question

The spring constant for the spring in a special cannon is 1800 N/m. In cocking the cannon, the spring is compressed 0.55 m. What is the initial speed of a 7.0 kg cannonball at rest on the free end of the spring when it is released? 1) 77 m/s 2) 45 m/s 3) 30 m/s 4) 15 m/s

Answer 1

The initial speed of the cannonball is 15 m/s.(Option 4)

Step-by-step explanation:

To find the initial speed of the cannonball, we can use the formula for potential energy stored in a spring: PE =
`(1/2)kx^2`, where PE is the potential energy, k is the spring constant, and x is the compression distance. We can set the potential energy equal to the kinetic energy of the cannonball when it is released from the spring:
`(1/2)mv^2`, where m is the mass of the cannonball and v is its velocity. We can solve for v by equating and rearranging the equations:

`(1/2)kx^2 = (1/2)mv^2`

`v = √((k/m)x^2)`

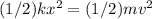
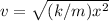
Plugging in the given values of k = 1800 N/m, x = 0.55 m, and m = 7.0 kg, we get:

v =
`√(((1800 N/m)/(7.0 kg) * (0.55 m)^2))` = 15 m/s

Therefore, the initial speed of the cannonball is 15 m/s (Option 4).