To find a point of constructive interference between the two speakers, we need to ensure that the sound waves from both speakers arrive at this point in phase. Constructive interference occurs when the path length difference between the waves from the two speakers is an integer multiple of the wavelength
 , where
, where
 is an integer and
is an integer and
 is the wavelength).
is the wavelength).
Let's consider a point
 on the x-axis between the origin (0,0) and the speaker on the x-axis. We need to find the value of
on the x-axis between the origin (0,0) and the speaker on the x-axis. We need to find the value of
 where the path length difference between the sound waves from the two speakers to point
where the path length difference between the sound waves from the two speakers to point
 meets the condition for constructive interference.
meets the condition for constructive interference.
1. Calculate the Distance from Each Speaker to Point P :
- Distance from the first speaker at (0, 2.3) to P:

- Distance from the second speaker at (6.6, 0) to P:

2. Path Length Difference :
The path length difference

3. Constructive Interference Condition :
For constructive interference,
 . Since we are not given the wavelength and the frequency, we assume the simplest case where
. Since we are not given the wavelength and the frequency, we assume the simplest case where
 for the first point of constructive interference. Thus,
for the first point of constructive interference. Thus,
 .
.
4. **Setting Up the Equation**:
![\[ |6.6 - x| - √(x^2 + (2.3)^2) = 0 \]](https://img.qammunity.org/2024/formulas/physics/high-school/9b7o8k98744dqw524bshfga067y28vhbuh.png)
5. Solving for x :
This requires solving the equation to find the value of
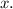
Let's perform the calculation.
The symbolic solver encountered a difficulty with the absolute value function in the equation. To resolve this, we can consider the problem in two separate cases based on the range of
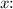
1. Case 1 :

2. Case 2 :

Since we are looking for a point between (0,0) and the speaker on the x-axis (6.6, 0), we will focus on Case 1. The equation becomes:
![\[ 6.6 - x - √(x^2 + 2.3^2) = 0 \]](https://img.qammunity.org/2024/formulas/physics/high-school/hxoligazalpg9ah0gnmptdolnlp25u9kco.png)
Now, let's solve this equation to find the value of
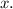
For the case where
 the value of
the value of
 at a point of constructive interference between the two speakers is approximately
at a point of constructive interference between the two speakers is approximately
 meters.
meters.
This is the x-coordinate of the first point on the x-axis between (0,0) and the speaker at (6.6, 0) where constructive interference occurs, assuming the simplest case of
