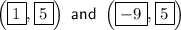Answer:
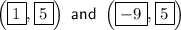
Explanation:
Given:
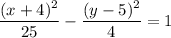
To find:
Coordinate of the vertices
Solution:
The given equation represents a hyperbola in standard form.
To find the coordinates of the vertices, we can compare it to the general equation for a hyperbola with a horizontal major axis:

In this case, we have:
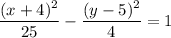
We can see that the center of the hyperbola is at the point (-4, 5), which is represented by (h, k) in the general equation.
Now, we can determine the values of a and b:
a² = 25, so a = 5
b² = 4, so b = 2
The coordinates of the vertices are (h ± a, k), so for this hyperbola:
Vertices: (-4 ± 5, 5)
The two vertices are:
Vertex A: (-4 + 5, 5) = (1, 5)
Vertex B: (-4 - 5, 5) = (-9, 5)
So, the coordinates of the vertices of the hyperbola are: