Question

What are the coordinates of point B on AC such that the ratio of AB to BC is 5 : 6

Answer 1

We have a segment AC, with the point B lying between A and C.

The ratio AB to BC is 5:6.

The coordinates for A and C are:

A=(2,-6)

C=(-4,2)

We can calculate the coordinates of B for each axis, using the ratio of 5:6.

`\begin{gathered} (x_a-x_b)/(x_b-x_c)=(2-x_b)/(x_b+4)=(5)/(6)_{} \\ 6\cdot(2-x_b)=5\cdot(x_b+4) \\ 12-6x_b=5x_b+20 \\ -6x_b-5x_b=20-12_{} \\ -11x_b=8 \\ x_b=-(8)/(11)\approx-0.72\ldots \end{gathered}`

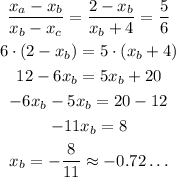
We can do the same for the y-coordinates:

`\begin{gathered} (y_a-y_b)/(y_b-y_c)=(-6-y_b)/(y_b-2)=(5)/(6) \\ 6(-6-y_b)=5(y_b-2) \\ -36-6y_b=5y_b-10 \\ -6y_b-5y_b=-10+36 \\ -11y_b=26 \\ y_b=-(26)/(11)\approx-2.36\ldots \end{gathered}`

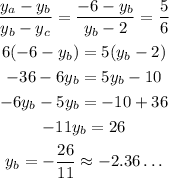
The coordinates of B are (-8/11, -26/11).