Question

What is the absolute minimum and maximum of y=2x-1

Answer 1

No specific values

Explanation:

To find the absolute minimum and maximum of y=2x-1, we can use the following formulas:

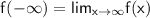
• Absolute minimum:

`\sf f(-\infty) = lim_(x \to \infty) f(x)`

Absolute maximum:

`\sf f(\infty) = lim_(x \to \infty) f(x)`

Substituting the function f(x) = 2x-1 into the formulas, we get:

Absolute minimum:

`\sf f(-\infty) = lim_(x \to \infty) f(x) =-\infty`

Absolute maximum:

`\sf f(\infty) = lim_(x \to \infty) f(x) =\infty`

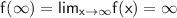
Therefore, the absolute minimum of y=2x-1 is -∞, and the absolute maximum of y=2x-1 is ∞.

Since, the range of y for this function is (-∞, ∞), which means it can take any real value, and there are no specific minimum or maximum values for y in the real number system.

Answer 2

No absolute minimum or maximum.

Explanation:

The absolute minimum is the smallest output value the function can have for any input within its defined domain.

The absolute maximum is the largest output value the function can have for any input within its defined domain.

The linear function y = 2x - 1 does not have an absolute minimum or maximum because there are no specific constraints on its domain or range and so it continues indefinitely in both directions. The function can have values that are as low or as high as desired, and there is no absolute minimum or maximum within the real number line for this function.