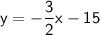Question

What is the equation of the line –3x–2y=30 in slope-intercept form?

I do not have a graph, so it might be hard for you all.

Answer 1

`\sf y = - (3)/(2)x - 15`

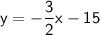
Explanation:

The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.

The slope of a line tells us how steep the line is, and the y-intercept tells us where the line crosses the y-axis.

To convert the equation –3x–2y=30 to slope-intercept form, we can use the following steps:

Add 3x to both sides of the equation:

`\sf - 3x–2y + 3x = 30 + 3x`

`\sf -2y = 30 + 3x`

Divide both sides of the equation by –2:

`\sf (-2y )/(2 )= (30 + 3x)/( -2)`

`\sf y = -15 - (3)/(2)x`

`\sf y = - (3)/(2)x - 15`

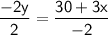
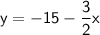
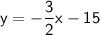
Therefore, the equation of the line in slope-intercept form is:

`\sf y = - (3)/(2)x - 15`

Answer 2

`y=-(3)/(2)x-15`

Explanation:

Slope-intercept form is a linear equation written in the form y = mx + b, where m is the slope of the line, and b is the y-intercept.

To express the equation -3x - 2y = 30 in slope-intercept form, use algebraic operations to isolate y.

Begin by adding 3x to both sides of the equation:

`\begin{aligned}-3x-2y+3x&=30+3x\\\\-2y&=3x+30\end{aligned}`

Now, divide both sides of the equation by -2 to isolate y:

`\begin{aligned}(-2y)/(-2)&=(3x)/(-2)+(30)/(-2)\\\\y&=-(3)/(2)x-15\end{aligned}`

So, the given equation in slope-intercept form is:

`\large\boxed{\boxed{y=-(3)/(2)x-15}}`