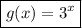Question

G(2) = type your answer...

g(x) = 3, x = type your answer...
g(0) = type your answer...
Write the rule for g(x): g(x) = type your a
)^x
L

Answer 1

`g(2) = 9`

`x = 1`

`g(0) = 1`

`g(x)=3^x`

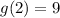
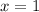
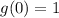
Explanation:

To find g(2), find the y-value when x = 2.

From inspection of the graph, g(2) = 9.

To find x when g(x) = 3, find the x-value when y = 3.

From inspection of the graph, g(1) = 3, so x = 1.

To find g(0), find the y-value when x = 0.

From inspection of the graph, g(0) = 1.

Therefore, we have determined the following ordered pairs:

• (0, 1)
• (1, 3)
• (2, 9)

The given graph is a graph of an exponential function.

General form of an exponential function:

`f(x)=ab^x`

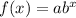
where:

• a is the initial value (y-intercept).
• b is the base (growth/decay factor) in decimal form.

The y-intercept is when x = 0.

As the y-intercept is 1, a = 1:

`\implies g(x)=(1)b^x`

`\implies g(x)=b^x`

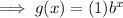
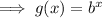
To find the value of b, substitute one of the ordered pairs into the function and solve for b:

`\begin{aligned}g(x)=b^x&\phantom{=}\\\implies g(2)=b^2&=9\\ √(b^2)&=√(9)\\b&=3\end{aligned}`

Therefore, the rule for the graphed function is:

`\boxed{g(x)=3^x}`