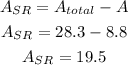Question

Find the area of the shaded region.3112Note: Use either the pi button on your calculator or 3.14 for pi. Round to the nearest tenth.

Answer 1

The area of a sector of a circle can be calculated by using the formula:

`A=(\theta)/(360)\cdot\pi\cdot r^2\text{ where }\theta\text{ is the angle in degrees and r is the radius}`

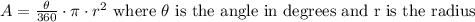
The total area of a circle can be calculated as:

`A_(total)=\pi\cdot r^2\text{ where r is the radius}`

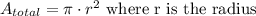
To find the area of the shaded region, you need to calculate the total area of the circle and then subtract the area of the non-shaded region, as follows:

`\begin{gathered} A_(total)=\pi\cdot r^2\text{ The given value for r is 3} \\ A_(total)=\pi\cdot3^2\text{ } \\ A_(total)=\pi\cdot9 \\ A_(total)=3.14\cdot9 \\ A_(total)=28.3 \end{gathered}`

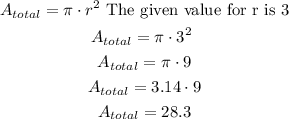
Now let's calculate the area of the non-shaded region:

`\begin{gathered} A=(\theta)/(360)\cdot\pi\cdot r^2\text{ the given values for }\theta=112\text{ and r=3} \\ A=(112)/(360)\cdot\pi\cdot3^2\text{ } \\ A=0.31\cdot3.14\cdot9 \\ A=8.8 \end{gathered}`

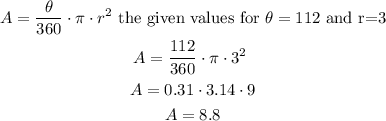
The area of the shaded region will be:

`\begin{gathered} A_(SR)=A_(total)-A \\ A_(SR)=28.3_{}-8.8 \\ A_(SR)=19.5 \end{gathered}`