Question

When will the firework land if it does not explode?

(What is the height of the firework when it lands on the ground… plug that in for height and solve for t.. You are looking for an x-intercept.. YOU MUST SHOW WORK FOR THIS QUESTION)
given:
h(t) = -16t^2 + 150t + 70
(t is time, 70 is height, 150t is the velocity of the firework)

Answer 1

9.8 seconds

Explanation:

The height of the firework when it lands (given it does not explode) is zero meters. Therefore, to find out when the firework will land, set h(t) equal to 0 and solve for t:

`-16t^2 + 150t + 70 = 0`

To solve this quadratic equation, we can use the quadratic formula:

`\boxed{\begin{array}{l}\underline{\sf Quadratic\;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\textsf{when} \;ax^2+bx+c=0 \\\end{array}}`

In this case:

• x = t
• a = -16
• b = 150
• c = 70

Substitute the values into the quadratic formula:

`t=(-(150) \pm √((150)^2-4(-16)(70)))/(2(-16))`

Solve for t:

`t=(-150 \pm √(22500+4480))/(-32)`

`t=(150 \pm √(26980))/(32)`

Therefore, the two possible values of t are:

`t=9.8204968...`

`t=-0.4454968...`

In this context, time cannot be negative. Therefore, the positive value of t represents the time it takes for the firework to land.

So, the firework will land 9.8 seconds after it is fired (rounded to the nearest tenth).

Answer 2

9.82049680 seconds

Explanation:

We know that the firework lands when the height is equal to 0.

So, we can set h(t) equal to 0 and solve for t.

`\sf h(t) = -16t^2 + 150t + 70 = 0`

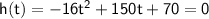
We can use the quadratic formula to solve for t:

`\sf t = (-b \pm √(b^2 - 4ac))/(2a)`

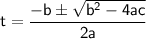
where a = -16, b = 150, and c = 70.

Substitute the known value and simplify.

`\sf t = (-150 \pm √(150^2 - 4 \cdot (-16) \cdot( 70)))/(2 \cdot -16)`

`\sf t = (-150 \pm √(22500 + 4480))/(-32)`

`\sf t = (-150 \pm √(26980))/(-32)`

`\sf t = (-150 \pm 2 √(6745))/(-32)`

`\sf t = 2\left( (-75 \pm √(6745))/(-32) \right)`

`\sf t = (-75 \pm √(6745))/(-16)`

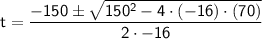
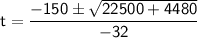
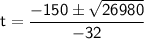
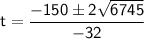
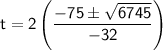
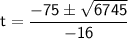
We have two possible solutions:

When Positive:

`\sf t = (-75 + √(6745))/(-16) \approx -0.4454968`

When negative

`\sf t = (-75 - √(6745))/(-16) \approx 9.82049680`

Since the firework cannot land before it is launched, we can discard the negative solution.

Therefore, the firework will land at t = 9.82049680 seconds.