Question

Please help meee!!!!!!
​

Answer 1

a. In this context, the domain is the set of all possible input values or x-values.

Since x represents the time in minutes, it cannot be negative.

Therefore, the domain is the set of all non-negative real numbers, or [0, ∞).

The range is the set of all possible output values or y-values.

Since y represents the altitude in feet, it should also be non-negative and cannot be more than the initial altitude of the paraglider which is 1000 feet.

Moreover, the paraglider lands at a site 100 feet above sea level. Therefore, the range is [100, 1000].

To graph the function, plot the y-intercept at (0, 1000) and use the slope to find another point on the graph.

The slope is -200, meaning for every minute (x), the altitude (y) decreases by 200 feet.

So after 1 minute, the paraglider will be at an altitude of 800 feet.

Plot this point (1, 800) and draw a line through the points.

b. The slope of the graph is -200.

This indicates that for every minute, the paraglider descends 200 feet.

This is a negative slope, which correlates to the fact that the paraglider is descending.

The y-intercept is 1000, meaning that when the paraglider starts (at time x = 0), the altitude is 1000 feet.

The x-intercept will be the time when the paraglider reaches the landing site, 100 feet above sea level.

To find this, set f(x) = 100 and solve for x. Doing so gives x = 4.5, so the paraglider lands after 4.5 minutes.

c. To find out who reaches an altitude of 100 feet first, set both equations equal to 100 feet and solve for x.

For the first paraglider:

-200x + 1000 = 100
-200x = -900
x = 4.5 minutes

For the second paraglider:

-150x + 900 = 100
-150x = -800
x = 800/150 = 5.333 minutes

Therefore, the first paraglider reaches the altitude of 100 feet first, after 4.5 minutes, while the second paraglider does so after approximately 5.33 minutes.

Answer 2

(a) Domain = [0, 4.5]
Range = [100, 1000]
See the attachment for the graph.

(b) Slope: Rate of descent (-200 ft per minute)
y-intercept: Initial altitude of the paraglider (1000 ft)

(c) The first paraglider reaches an altitude of 100 ft first.

Explanation:

The function f(x) = -200x + 1000 represents the altitude (in feet) of a paraglider x minutes from the time the paraglider begins a descent to a landing site located 100 feet above sea level.

`\hrulefill`

Part (a)

The domain of a function is the set of all possible input values (x-values) for which the function is defined. In this context, x represents the time (in minutes), so it must be a positive value since time cannot be negative. The maximum value of x is when y is at its smallest possible value, which is when the paraglider lands when y = 100. Therefore, the domain is [0, 4.5].

The range of a function is the set of all possible output values (y-values) for which the function is defined. In this context, the range represents the possible altitudes (in feet) of the paraglider. The altitude starts at 1000 feet above sea level and decreases as the paraglider descends to 100 feet above sea level. Therefore, the range is [100, 1000].

To graph the function on the given coordinate plane:

• Number the x-axis from 0 to 9 in increments of one.
• Number the y-axis from 100 to 1000 in increments of 100.
• Plot the y-intercept at point (0, 1000).
• Plot point (4.5, 100).
• Draw a straight line connecting the points.

`\hrulefill`

Part (b)

The slope of the graph of f(x) is -200, which represents the rate of descent. Therefore, the paraglider is descending at a rate of 200 feet per minute.

The y-intercept is 1000, which represents the initial altitude of the paraglider when the descent begins. The initial altitude is 1000 feet above sea level.

`\hrulefill`

Part (c)

The function g(x) = -150x + 900 represents the altitude (in feet) of a second paraglider x minutes from the time the paraglider begins a descent to the same landing site.

Both paragliders start their descent at the same time.

To determine who reaches an altitude of 100 feet first, set both functions equal to 100, and solve for x.

`\begin{aligned}f(x):\quad -200x+1000&=100\\-200x&=-900\\x&=4.5\; \sf minutes\end{aligned}`

`\begin{aligned}g(x):\quad -150x+900&=100\\-150x&=-800\\x&=5.3\; \sf minutes\;(1\;d.p.)\end{aligned}`

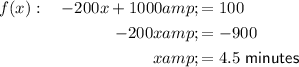
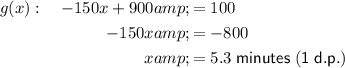
So, the first paraglider reaches an altitude of 100 feet at x = 4.5 minutes, while the second paraglider reaches the same altitude at x = 5.3 minutes.

Therefore, the first paraglider reaches an altitude of 100 feet first, since 4.5 is less than 5.3.