Question

Hhellp asap!!!!????????

Answer 1

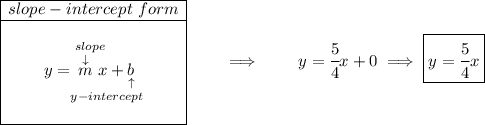
so hmm we know the line crosses the origin and it also passes through (4 , 5) as we can see in the picture below. To get the slope of any straight line, we simply need two points off of it, let's use those two points then

`(\stackrel{x_1}{0}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{4}~,~\stackrel{y_2}{5}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{5}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{4}-\underset{x_1}{0}}} \implies \cfrac{ 5 }{ 4 }`

now, we know it touches the y-axis at the origin, so that is the y-intercept.

`\begin{array}ll \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}\qquad \implies \qquad y=\cfrac{5}{4}x+0\implies \boxed{y=\cfrac{5}{4}x}`