Question

A national standard requires that public bridges over 20 foot in length must be inspected and rated overy 2 yours. The rating scalo ranges from 0 (poorest rating) to 9 (highost rating). A group of engineers used aprobabilistio model to forecast the inspection ratings of all major bridges in a city. For the year 2020, the enginoors forecast that 8% of all major bridges in that city will have ratings of 4 or below. Comploto parts aand bea. Use tho forecast to find the probability that in a random sample of 8 major bridgos in the city, at least 3 will have an inspection rating of 4 or below in 2020,PIX23) - (Round to five decimal places as needed.)

Answer 1

We can solve the problem by using the probability binomial distribution model. The formula is:

`P(X=x)=(^n_x)p^xq^(n-x)`

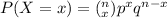
Recall that:

`(^n_x)=^nC_x`

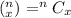
Given:

number of samples(n) = 8

x = 3

8% of all major bridges in that city will have ratings of 4 or below implying that the probability of a bridge having a rating of 4 or below is 0.08.

Hence,

`\begin{gathered} p\text{ = 0.08} \\ q\text{ = 1-p } \\ q\text{ = 1-0.08} \\ q\text{ = 0.92} \end{gathered}`

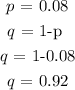
The probability that in a random sample of 8 major bridges in the city, at least 3 will have an inspection rating of 4 or below in 2020 would be:

`\text{Probability of at least 3 = 1 - Probability of at most }2`

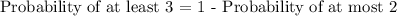
Probability of at most 2 can be reduced to:

`P(x\text{ }<\text{ 3) = P(x =2) + P(x = 1) + P(x = 0)}`

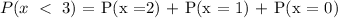
Evaluating the expression, we have:

`\begin{gathered} P(x\text{ }<3)=^8C_2(0.08)^2(0.92)^(8-2)+^8C_1(0.08)^1(0.92)^(8-1)+^8C_0(0.08)^0(0.92)^(8-0) \\ =\text{ 0.10866 + 0.35702 + }0.51322 \\ =\text{ 0.9789}0 \end{gathered}`

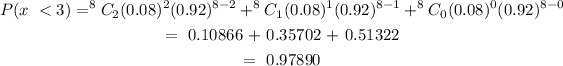
The probability that at least 3 will have a rating of 4 and below:

`\begin{gathered} P(x\text{ }\ge3)\text{ = 1 - P(x }<\text{ 3)} \\ =\text{ 1 - 0.97890} \\ =\text{ 0.02110} \end{gathered}`

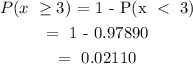
Answer:

0.02110