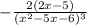Question

Please solve using chain rule

Answer 1

`g(x)=\cfrac{-1}{(x^2-5x-6)^2}\implies g(x)=-(x^2-5x-6)^(-2) \\\\\\ \cfrac{dg}{dx}=-\stackrel{ \textit{chain rule} }{(-2)(x^2-5x-6)^(-3)\cdot (2x-5)}\implies \cfrac{dg}{dx}=\cfrac{2(2x-5)}{(x^2-5x-6)^3}`

Answer 2

Explanation:

First we will bring up the denominator using the negative exponent rule, giving us -(x^2-5x-6)^-2.

Then, to find the derivative, we will...

take the derivative of the outer function, which is
`x^{-2`

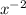
the derivative of this is
`-2x^(-3)`

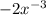
into the x, we replace the inner function, giving us
`-2(x^2-5x-6)^(-3)`

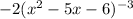
Now, we must multiply this with the derivative of the outer function, which is
`2x-5`

So, we have
`-2(x^2-5x-6)^(-3)*(2x-5)`

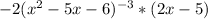
We can bring the portion with the -3 exponent back to the denominator and turn it positive again, giving us
`-(2(2x-5))/((x^2-5x-6)^3)`.

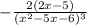Thus, g'(x)=
`-(2(2x-5))/((x^2-5x-6)^3)`