Question

What is the GCF of a¹²b⁴, a⁴b⁸, a²⁴b¹⁶ and a¹²b²⁰?​

Answer 1

Given:

a¹²b⁴, a⁴b⁸, a²⁴b¹⁶ and a¹²b²⁰.

To find:

The GCF of given terms.

Solution:

Greatest common factor (GCF): To find the GCF of two or more numbers, we need to find the product of their prime factor with their maximum powers.

The given terms are

`a^(12)b^(4),a^(4)b^8, a^(24)b^(16), a^(12)b^(20)`

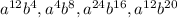
Here, each term has two prime factors a and b. The highest power of a is 24 and the highest power of b is 20. So, the GCF of given terms is

`GCF=a^(24)* b^(20)`

`GCF=a^(24)b^(20)`

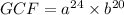
Therefore, the GCF of a¹²b⁴, a⁴b⁸, a²⁴b¹⁶ and a¹²b²⁰ is a²⁴b²⁰.