Question

24. The area of a square garden is 128 m². How long is the diagonal?

86 m
16m
432 m
8m

Answer 1

16 m

Explanation:

Given the area of the square garden, we can determine the length of its diagonal using the following steps:

Step 1: Determine the length of one side:

The formula for the area of a square is given by:

`A=s^2`, where:

• A is the area in units squared,
• and s is the length of the sides.

Thus, we can length of the square garden's sides by substituting 128 for A in the area formula:

`128=s^2\\\\√((128))=√((s^2))\\ \\ √((64*2))=√((s^2))\\ \\ 8√(2)=s`

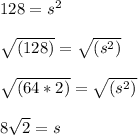
Thus, the square has a side length of 8√2 meters.

Step 2: Find the length of the square garden's diagonal using the Pythagorean Theorem:

• A square has four equal sides and four right angles.
• A square's diagonal creates two right angles between the diagonal.

• Since the diagonal is always opposite the right angle, it's the hypotenuse.

Given two sides of a right triangle, you can find the length of the third side (in this case, the diagonal) using the Pythagorean Theorem, which is given by:

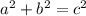`a^2+b^2=c^2`, where:

• a and b are the length of the legs (i.e., the shortest sides),
• and c is the length of the hypotenuse (i.e., the longest sides).

Since the two legs are both 8√2 meters long, we can solve for c (the length of the diagonal) by substituting 8√2 for a and b in the Pythagorean Theorem:

`(8√(2))^2+(8√(2))^2=c^2\\ \\ 128 + 128 = c^2\\\\√((256))=√((c^2)) \\\\16=c`

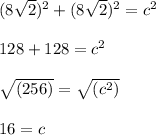
Therefore, the square garden's diagonal is 16 meters long.