Question

Which is the interval(s) on which the function f(x) = x³ + 2x² - 4x - 8 is increasing?

Answer 1

differentiate f(x)

power rule:
`(d)/(dx) x^n=nx^(n-1)`

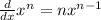
constant rule:
`(d)/(dx) (n)=0`

`f'(x)=(d)/(dx)(x^3+2x^2-4x-8)\\\\= (d)/(dx) (x^3)+2(d)/(dx)(x^2)-4(d)/(dx) (x)-(d)/(dx) (8)\\\\=3x^2+2(2x)-4(1)-0\\\\=3x^2+4x-4\\\\=(x+2)(3x-2)`

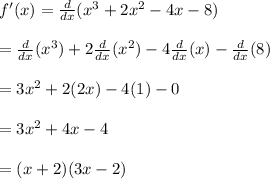
find x-intercepts:

x = -2, 2/3

intervals:

x < -2

-2 < x < 2/3

x > 2/3

take a number on each interval and plug it in the equation to see if it is positive or negative:

x < -2 --> x = -3

f'(-3) = (-3 + 2) · (3(-3) - 2)

= (-1) · (-11)

= 11

positive!

-2 < x < 2/3 --> x = 0

f'(0) = (0 + 2)(3(0) - 2)

= (2) · (-2)

= -4

negative!

x > 2/3 --> x = 1

f'(1) = (1 + 2)(3(1) - 2)

= 3 · 1

= 3

positive!

so, f(x) is increasing when x < -2 and x > 2/3, and decreasing when

-2 < x < 2/3.