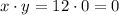Question

Among all of the pairs of numbers whose difference is 12, the smallest product is

Answer 1

We have two numbers x and y such that their difference is 12:

`\begin{gathered} x-y=12 \\ \Rightarrow x=12+y \end{gathered}`

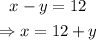
Now, we take the product of them:

`x\cdot y=(12+y)\cdot y=y^2+12y`

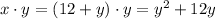
The smallest result we can get is 0 (ignoring the negative numbers, because the meaning of "small" implies an absolute value). Looking at the expression above, it is 0 for y = 0. If y = 0 then x = 12, and the difference is:

`x-y=12-0=12`

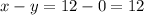
And their product is:

`x\cdot y=12\cdot0=0`