Question

If you roll a fair 6 sided die and then roll a second fair what is the probability that you roll 1, 2, or 3 on the first die and roll 5 on second

Answer 1

Given:

A fair 6 sided die is rolled and then a second fair die is rolled.

To find:

The probability that you roll 1, 2, or 3 on the first die and roll 5 on second.

Solution:

If two fair die are rolled, then the total possible outcomes are

S= {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}

So, total outcomes = 36.

Favorable outcomes of getting 1, 2, or 3 on the first die and roll 5 on second are (1,5), (2,5), (3,5).

So, favorable outcomes = 3

We know that

`\text{Probability}=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

`\text{Probability}=(3)/(36)`

`\text{Probability}=(1)/(12)`

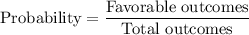
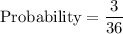
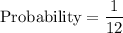
Therefore, the required probability is
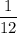`(1)/(12)`.