Answer:
13. t = 1183 min and 0.50 M.
14.
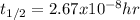
Step-by-step explanation:
Hello!
13. In this case, according to the units, we infer this is a second-order reaction which has the following integrated rate law:
![(1)/([A]) =(1)/([A]_0) +kt](https://img.qammunity.org/2022/formulas/chemistry/college/3hy5v6y559513rfsaybpbyvcsskxoixdbb.png)
Which can be solved for the time as shown below:
![t=( (1)/([A])-(1)/([A]_0))/(k)](https://img.qammunity.org/2022/formulas/chemistry/college/87855pzt3ec7jh40wv1g23jx8ypxoaf0h1.png)
Thus, we plug in the given concentrations and rate constant to obtain:

For the second part, we proceed by using the same rate constant and the new initial concentration as follows:
![(1)/([A]) =(1)/([A]_0) +kt\\\\(1)/([A]) =(1)/(0.750M) +0.680M^(-1)min^(-1)*0.996min\\\\(1)/([A]) =1.99,M](https://img.qammunity.org/2022/formulas/chemistry/college/97bxie3anmf7pa6igvii04ze03x30ddmeq.png)
![[A]=0.50M](https://img.qammunity.org/2022/formulas/chemistry/college/s0sk3j8irifpbgcu4fosvej4yuzl9gm88w.png)
14. In this case, according to the units of the rate constant, we infer this is a zeroth-order reaction, therefore we compute the half-life has shown below:
![t_(1/2)=([A]_0)/(2k)](https://img.qammunity.org/2022/formulas/chemistry/college/qf7rvybb2ruwosnn65ozl45h327bec54k2.png)
Thus, we plug in to obtain:
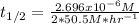
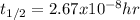
Best regards!