Question

starting from ret, the car accelerates for 20s with constant linear acceleration of 0,800m/s2. the radius=0,330m of the wheel. what is the angle through which each wheel has rotated?

Answer 1

Approximately
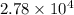`2.78 * 10^(4)` degrees (approximately
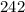`242` radians.)

Step-by-step explanation:

The rotation of the wheels can be found in the following steps:

• Apply the SUVAT equations of linear motion to find the linear distance travelled.
• Divide the linear distance travelled by radius
  `r` to find the angle of rotation.

Assuming that the vehicle started from rest, such that initial velocity would be
`u = 0\; {\rm m\cdot s^(-1)}`. At a constant linear acceleration of
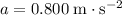`a = 0.800\; {\rm m\cdot s^(-2)}`, the linear displacement in
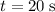`t = 20\; {\rm s}` would be:

`\begin{aligned}x &= (1)/(2)\, a\, t^(2) + u\, t \\ &= (1)/(2)\, (0.800)\, (20)^(2) \; {\rm m} \\ &= 160\; {\rm m}\end{aligned}`.

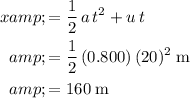Since the direction of motion of this vehicle stays the same, the distance travelled would be equal to the magnitude of linear displacement:
`160\; {\rm m}`.

Divide the linear displacement by the radius to find the angle of rotation, in radians:

`\begin{aligned}\theta &= (s)/(r) \\ &= \frac{160\; {\rm m}}{0.330\; {\rm m}} \\ &\approx 485\end{aligned}`.

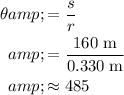In other words, the angle of rotation would be approximately
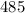`485` radians for each wheel.

Radians and degrees are both units of measurement of angles. The relation between the two is
`(2\, \pi) \; \text{radian} = 360^(\circ)`. Multiply the angle of rotation in radians by
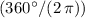`(360^(\circ) / (2\, \pi))` to find the measurement in degrees:

`\displaystyle \theta \approx 485 * (360)/(2\, \pi) \approx 2.78 * 10^(4)`.

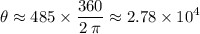In other words, the angle of rotation is approximately.
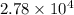`2.78 * 10^(4)` degrees.