Question

a 76.0-kg person is being pulled away from a burning building asshown infigure 4.41. calculate the tension in the two ropes if the personis momentarily motionless. include a free-body diagram in your solution

Answer 1

The tensions in the ropes are
`\( T_1 = 1737.34 \)` N and
`\( T_2 = 1704.03 \)` N to hold the 76.0 kg person motionless.

To solve this problem, we need to apply the principles of static equilibrium, where the sum of forces in any direction and the sum of moments about any point are zero. The person is stationary, which means the net force on the person is zero.

The forces acting on the person are:

1. The gravitational force
`(\( W \))`, which is the weight of the person acting downward.

2. The tension in rope 1
`(\( T_1 \))`, which acts at an angle of 15 degrees to the horizontal.

3. The tension in rope 2
`(\( T_2 \))`, which acts at an angle of 10 degrees to the horizontal.

From the diagram, we can denote the angles as follows:

• 
  `\( \theta_1 = 15^\circ \) (angle for \( T_1 \))`

• 
  `\( \theta_2 = 10^\circ \) (angle for \( T_2 \))`

The weight
`\( W \)` can be calculated using the mass
`(\( m \))` and the acceleration due to gravity
`(\( g \))`, which is approximately
`\( 9.81 \text{ m/s}^2 \)`:

• 
  `\[ W = m \cdot g \]`

• 
  `\[ W = 76.0 \text{ kg} \cdot 9.81 \text{ m/s}^2 \]`

Now, we can set up the equations for equilibrium. The sum of forces in the horizontal direction
`(\( \Sigma F_x \))` must be zero, and the sum of forces in the vertical direction
`(\( \Sigma F_y \))` must also be zero.

For the horizontal direction:

• 
  `\[ T_1 \cos(\theta_1) = T_2 \cos(\theta_2) \]`

• 
  `\[ T_1 \cos(15^\circ) = T_2 \cos(10^\circ) \](1)`

For the vertical direction:

• 
  `\[ T_1 \sin(\theta_1) + T_2 \sin(\theta_2) = W \]`

• 
  `\[ T_1 \sin(15^\circ) + T_2 \sin(10^\circ) = W \](2)`

Let's calculate the weight and then solve these two equations simultaneously for
`\( T_1 \)` and
`\( T_2 \)`.

Given the problem, we need to balance the forces in two dimensions. Since the person is momentarily motionless, the net force acting on them is zero both in the horizontal
`( $\left.\Sigma F_x\right)$` and vertical
`$\left(\Sigma F_y\right)$` directions.

Here are the equations we need to solve:

1. For the horizontal direction (left-right balance):

`$$T_1 \cdot \cos \left(15^(\circ)\right)=T_2 \cdot \cos \left(10^(\circ)\right)$$`

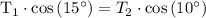
2. For the vertical direction (up-down balance):

`$$T_1 \cdot \sin \left(15^(\circ)\right)+T_2 \cdot \sin \left(10^(\circ)\right)=W$$`

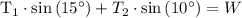
Given:

`$m=76.0 \mathrm{~kg}$` (mass of the person)

`$g=9.81 \mathrm{~m} / \mathrm{s}^2$` (acceleration due to gravity)

First, we calculate the weight
`$(W)$` of the person:

`$$\begin{aligned}& W=m \cdot g \\& W=76.0 \cdot 9.81\end{aligned}$$`

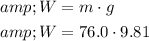
The tensions in the two ropes when the person is momentarily motionless are as follows:

• Tension in rope 1
  `(\( T_1 \))` is approximately
  `\( 1737.34 \)` N.
• Tension in rope 2
  `(\( T_2 \))` is approximately
  `\( 1704.03 \)` N.

The weight of the person, calculated using their mass and the acceleration due to gravity, is
`\( 745.56 \) N\\`.

The complete question and diagram is given below: