Question

100 POINTS: On the putting green, a golf ball travels at 1.3 m/s in a direction of 140°. The ball encounters wind blowing at 1.2 m/s in the direction of 50°. What is the true speed and direction of the ball? Round the speed to the thousandths place and direction to the nearest degree.

A. 1.769 m/s; 83°
B. 1.769 m/s; 97°
C. 1.740 m/s; 83°
D. 1.740 m/s; 97°

Answer 1

B. 1.769 m/s; 97°

Explanation:

To find the true speed and direction of the golf ball's motion when affected by both its initial velocity and the wind, we can use vector addition. This can be done by breaking down the velocities into their horizontal (x) and vertical (y) components and then adding those components separately.

Find the horizontal and vertical components of both the golf ball's velocity and the wind velocity.

Golf ball (b)

`b_x=-1.3 \cos(40^(\circ))`

`b_y=1.3 \sin(40^(\circ))`

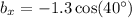
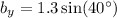
Wind (w)

`w_x=1.2 \cos(50^(\circ))`

`w_y=1.2 \sin(50^(\circ))`

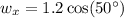
Now, add the horizontal and vertical components.

Horizontal component of the resultant velocity (R):

`R_x = b_x + w_x`

`R_x=-1.3 \cos(40^(\circ))+1.2 \cos(50^(\circ))`

`R_x\approx -0.225\;\sf (3\;d.p.)`

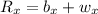
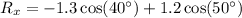
Vertical component of the resultant velocity (R):

`R_y= b_y + w_y`

`R_y=1.3 \sin(40^(\circ))+1.2 \sin(50^(\circ))`

`R_y\approx 1.755\;\sf (3\;d.p.)`

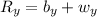
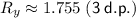
To determine the true speed of the ball, calculate the magnitude of the resultant vector (R) using the Pythagorean theorem:

`|R|=√((R_x)^2+(R_y)^2)`

`|R|=\sqrt{(-1.3 \cos(40^(\circ)) + 1.2 \cos(50^(\circ)))^2+(1.3 \sin(40^(\circ)) + 1.2 \sin(50^(\circ)))^2}`

`|R|=1.76918060...`

`|R|=1.769\; \sf m/s\;(3\;d.p.)`

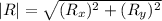
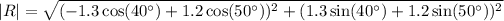
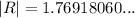
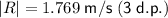
Therefore, the true speed of the ball is 1.769 m/s (rounded to the nearest thousandth).

When the horizontal component of the resultant velocity is negative, we should calculate the direction (θ) as 180° minus the arctan of the ratio of the vertical and horizontal components of the resultant velocity. This ensures the direction is relative to the positive x-axis.

`\theta = 180^(\circ)-\arctan\left|(R_y)/(R_x)\right|`

`\theta = 180^(\circ)-\arctan\left|(1.3 \sin(40^(\circ))+1.2 \sin(50^(\circ)))/(-1.3 \cos(40^(\circ))+1.2 \cos(50^(\circ)))\right|`

`\theta = 180^(\circ)-\arctan\left|-7.81638481... \right|`

`\theta = 180^(\circ)-\arctan\left(7.81638481... \right)`

`\theta = 180^(\circ)-82.7093899...^(\circ)`

`\theta=97^(\circ)\; \sf (nearest\;degree)`

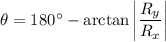
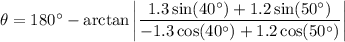
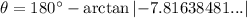
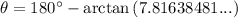
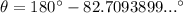
Therefore, the direction of the golf ball is 97° counterclockwise from the positive x-axis.