Question

Need help asap and show steps

Answer 1

Explanation:

You have the -5 cos part correct.....

the usual period for the cos function is 2 pi

this one has been stretched to 8 pi

which is stretched out 4 times making it 1/4 x

-5 cos ( x/4 )

Answer 2

`y = -5 \cos \left((1)/(4)x\right)`

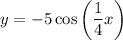
Explanation:

The standard form of a cosine function is:

`f(x) = A \cos(B(x + C)) + D`

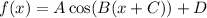
where:

• |A| is the amplitude (vertical height from the midline to the peak).
• 2π/B is the period (horizontal distance between consecutive peaks).
• C is the phase shift (horizontal shift - positive is to the left).
• D is the vertical shift.

The graph of the parent cosine function y = cos(x) has a local maximum at (0, 1). When reflecting the cosine function in the x-axis, it transforms into a graph with a local minimum at (0, -1), resembling the general shape of the given graph. This reflection is achieved by simply negating the function, resulting in y = -cos(x).

The amplitude of a cosine function is the distance from its midline to its peak or trough. In the case of the graphed function, the midline is the x-axis and the maximum y-value is 5. Therefore, the amplitude of the graphed function is 5. Consequently, we now have y = -5cos(x).

The period of a cosine function is the length of one complete cycle, which is the horizontal distance it takes for the function to repeat its values, such as from one peak to the next peak or one trough to the next trough. From observation of the graph, it is evident that the period of the graphed function is 8π. The coefficient of x (ω) can be calculated by dividing 2π by the period. Therefore, the value of ω for the graphed function is:

`\omega=(2 \pi)/(T)=(2 \pi)/(8\pi)=(1)/(4)`

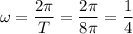
As there are no horizontal or vertical shifts, the equation of the graphed function can be expressed as:

`\large\boxed{\boxed{y = -5 \cos \left((1)/(4)x\right)}}`