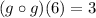Question

Use the table of values for f and g below to find the indicated compositions. (f \circ g)(8) =Answerg(f(3))=Answerf(f(1))=Answer (g \circ g)(6) =Answer

Answer 1

In order to find the value of a composition of functions at x = a, (f º g)(a), we first find the value of g(a), then find the value of f(x) at x = g(a).

(f º g)(a) = f(g(a))

In this problem, the values of f(x) and g(x) are shown in the table, for integer values of x from 0 to 9.

So, we have:

1. (f º g)(8) = f(g(8))

From the table, we see that

g(8) = 4 (value of g(x) in the line corresponding to x = 8)

Then:

f(g(8)) = f(4) = 4 (value of f(x) in the line corresponding to x = 4)

Thus:

`\mleft(f\circ g\mright)\mleft(8\mright)=4`

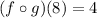
2. g(f(3))

f(3) = 8

g(8) = 4

Thus:

`g(f(3))=4`

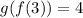
3. f(f(1))

f(1) = 6

f(6) = 2

Thus:

`f(f(1))=2`

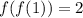
4. (g º g)(6) = g(g(6))

g(6) = 7

g(7) = 3

Thus:

`\mleft(g\circ g\mright)\mleft(6\mright)=3`