Answer:
37.6°
Explanation:
The given diagram shows triangle BCD. Since we have been given the lengths of all three sides of ΔBCD, we can use the Law of Cosines to find the measure of angle D.

In this case:
- Side b, opposite angle B, measures 18 m.
- Side c, opposite angle C, measures 15 m.
- Side d, opposite angle D, measures 11 m.
To calculate the measure of angle D, we can use the following formula:
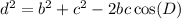
Substitute the side lengths into the equation and solve for D:

Therefore, the measure of angle D is approximately 37.6° (rounded to the nearest tenth).