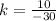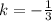Question

Which ordered pair would form a proportional relationship with the point graphed below?

Answer 1

`(x,y) = (-30,10)`

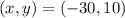
Explanation:

Given

`(x,y) = (60,-20)`

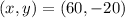
Required:

Determine a pair with a proportional relationship

A proportional relationship is:

`k = (y)/(x)`

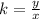
Where k is the constant of proportionality.

`(x,y) = (60,-20)`

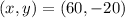
So, we have:

`k = (-20)/(60)`

`k = -(1)/(3)`

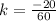
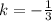
This means that for a pair to have a proportional relation, k must be -1/3.

This is true for (c).

Where:

`(x,y) = (-30,10)`

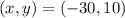
So, we have:

`k = (10)/(-30)`

`k = -(1)/(3)`