Question

Work out the equation of the perpendicular to 4x+3y=12 with a y-intercept of 5

Answer 1

`\sf y =(3)/(4)x+4`

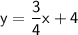
Explanation:

4x + 3y = 12

The equation of the given is in standard form. Write in slope-intercept form and find the slope of the given line.

Slope-y intercept form: y = mx + b

Where m is the slope and b is the y-intercept.

4x + 3y = 12

3y = -4x + 12

`\sf y = (-4)/(3)x+(12)/(3)\\\\y = (-4)/(3)x + 4`

`\text{Slope of the given line} \ m_1 = (-4)/(3)`

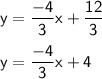
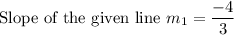
Product of the slope of the two perpendicular line is (-1 ).

`\sf m_1*m_2 = -1\\\\m_2 = (-1)/(m_1)\\\\m_2 = -1 / (-4)/(3)\\\\~~ = -1 *(-3)/(4)\\\\\boxed{\bf m_2 = (3)/(4)}`

Slope of the required perpendicular line is (3/4) and its y-intercept is 4.

Equation of the required line:

`\sf y =(3)/(4)x+ 4`