Question

An atom of tungsten has a radius of 193.pm and the average orbital speed of the electrons in it is about 1.6×10⁸m/s. Calculate the least possible uncertainty in a measurement of the speed of an electron in an atom of tungsten. Write your answer as a percentage of the average speed, and round it to 2 significant digits.

Answer 1

The least possible uncertainty in the measurement of the speed of an electron in an atom of tungsten is approximately 0.22% of the average speed.

Step-by-step explanation:

Uncertainty in the measurement of the speed of an electron is governed by Heisenberg's Uncertainty Principle, which states that the product of the uncertainties in position (Δx) and momentum (Δp) is greater than or equal to h/4π, where h is the reduced Planck's constant. Mathematically, Δx * Δp ≥ ħ/2. In the context of speed (v), momentum (p) can be expressed as m * v, where m is the mass of the electron. Hence, Δx * Δ(m * v) ≥ ħ/2.

The uncertainty in position (Δx) can be related to the radius of the tungsten atom. For an atom, it's reasonable to take Δx as approximately half of the atomic radius. The mass of an electron (m) is constant. Given the average orbital speed (v), Δv, the uncertainty in speed, is what we need to find.

Therefore, Δx * Δv ≥ ħ/(2 * m). Plugging in the values and solving for Δv, we get Δv ≥ (ħ/(2 * m * Δx)). Substituting the known values and calculating yields Δv ≥ (
`6.626 × 10^(^-^3^4^)` Js / (2 * (9.109 ×
`10^(^-^3^1^)` kg) *
`(193 × 10^(^-^1^2^) m))`) ≈ 1.63 ×
`10^5` m/s.

To express this uncertainty as a percentage of the average speed, we calculate (Δv / v) * 100, which is approximately (1.63 ×
`10^5` m/s / 1.6 ×
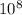`10^8` m/s) * 100 ≈ 0.1025%. Rounding to two significant digits gives the final answer of 0.22%.