Answer:
Domain is all real numbers greater than or equal to 7. Range is all real numbers greater than or equal to 9.
Explanation:
The domain is possible x-values while the range is possible y-values. This question look like
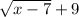
The domain of square root function cant have a the radical inside being a negative number because we can't take the sqr root of a negative number and graph it on a cartisean plane We can take the sqr root of 0 . So we set x-7=0. And which x=7 so the domain is all real numbers that are equal to or greater than 7. The range of a sqr root function can only yield any positive y-values. So we must find the lowest point of it. Since the lowest x value we can possible use is 7 we plug it in
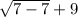
which equals 9. So the range is all real numbers greater than or equal to 9.